131 勾配の計算 代数的 vs 数値的¶
代数計算機 Sympyによる勾配の導出¶
In [1]:
%reload_ext autoreload
%autoreload 2
import sympy as sy
sy.init_printing(use_latex=True)
import autograd.numpy as np
from autograd import grad, jacobian, hessian
import inspect
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
% matplotlib inline
import multiprocessing as mp
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
変数定義¶
\begin{align}
f(x) &= \frac{1}{2}x^TQx + bx, \\
where \\
x &= [x_1, x_2, \cdots, x_j]^T, \\
b &= [b_1, b_2, \cdots, b_j], \\
Q &= \left[
\begin{array}{aaaa}
q_{11} & q_{12} & \ldots & q_{1j} \\
q_{21} & q_{22} & \ldots & q_{2j} \\
\vdots & \vdots & \ddots & \vdots \\
q_{i1} & q_{i2} & \ldots & q_{ij}
\end{array}
\right].
\end{align}
In [2]:
# Case-1
x_mat = sy.Matrix(2, 1, sy.symbols('x:2:1'))
Q_mat = sy.Matrix(2, 2, sy.symbols('Q:2:2'))
b_mat = sy.Matrix(1, 2, sy.symbols('b:1:2'))
f_mat = sy.Function('f_mat')(x_mat)
f_mat = ((1/2) *x_mat.T*Q_mat*x_mat+b_mat*x_mat)
display(x_mat, Q_mat, b_mat)
display(Q_mat.det())
display(f_mat)
# Case-2
x = sy.MatrixSymbol('x', 2, 1)
Q = sy.MatrixSymbol('Q', 2, 2)
b = sy.MatrixSymbol('b', 1, 2)
f = sy.Function('f')(x)
eq = sy.Eq(f, (1/2) *x.T*Q*x+b*x)
display(x, Q, b, eq)
$$\left[\begin{matrix}x_{00}\\x_{10}\end{matrix}\right]$$
$$\left[\begin{matrix}Q_{00} & Q_{01}\\Q_{10} & Q_{11}\end{matrix}\right]$$
$$\left[\begin{matrix}b_{00} & b_{01}\end{matrix}\right]$$
$$Q_{00} Q_{11} - Q_{01} Q_{10}$$
$$\left[\begin{matrix}b_{00} x_{00} + b_{01} x_{10} + x_{00} \left(0.5 Q_{00} x_{00} + 0.5 Q_{10} x_{10}\right) + x_{10} \left(0.5 Q_{01} x_{00} + 0.5 Q_{11} x_{10}\right)\end{matrix}\right]$$
$$x$$
$$Q$$
$$b$$
$$f{\left (x \right )} = b x + 0.5 x^T Q x$$
代数的な微分¶
Hessianは失敗
It cannot work https://stackoverflow.com/questions/46953823/get-computational-graph-expression-of-symbolic-matrix-differentiation
In [3]:
try:
display([f_mat.diff(x) for x in x_mat])
except Exception as e:
display(e.args)
try:
jac_f = [f_mat.diff(x) for x in x_mat]
display([[jac.diff(xx) for jac in jac_f] for xx in x_mat])
except Exception as e:
display(e.args)
try:
display([sy.Derivative(f_mat, x) for x in x_mat])
except Exception as e:
display(e.args)
try:
display([sy.hessian(f_mat, x) for x in x_mat])
except Exception as e:
display(e.args)
$$\left [ \left[\begin{matrix}1.0 Q_{00} x_{00} + 0.5 Q_{01} x_{10} + 0.5 Q_{10} x_{10} + b_{00}\end{matrix}\right], \quad \left[\begin{matrix}0.5 Q_{01} x_{00} + 0.5 Q_{10} x_{00} + 1.0 Q_{11} x_{10} + b_{01}\end{matrix}\right]\right ]$$
$$\left [ \left [ \left[\begin{matrix}1.0 Q_{00}\end{matrix}\right], \quad \left[\begin{matrix}0.5 Q_{01} + 0.5 Q_{10}\end{matrix}\right]\right ], \quad \left [ \left[\begin{matrix}0.5 Q_{01} + 0.5 Q_{10}\end{matrix}\right], \quad \left[\begin{matrix}1.0 Q_{11}\end{matrix}\right]\right ]\right ]$$
$$\left [ \frac{\partial}{\partial x_{00}} \left[\begin{matrix}b_{00} x_{00} + b_{01} x_{10} + x_{00} \left(0.5 Q_{00} x_{00} + 0.5 Q_{10} x_{10}\right) + x_{10} \left(0.5 Q_{01} x_{00} + 0.5 Q_{11} x_{10}\right)\end{matrix}\right], \quad \frac{\partial}{\partial x_{10}} \left[\begin{matrix}b_{00} x_{00} + b_{01} x_{10} + x_{00} \left(0.5 Q_{00} x_{00} + 0.5 Q_{10} x_{10}\right) + x_{10} \left(0.5 Q_{01} x_{00} + 0.5 Q_{11} x_{10}\right)\end{matrix}\right]\right ]$$
('Improper variable list in hessian function',)
Autogradによる数値的な勾配の計算¶
\begin{align}
f(x) &= \frac{1}{2}x^TQx + bx, \\
\nabla f(x) &= Qx + b, \\
\nabla^2 f(x) &= Q.
\end{align}
パラメータに数値を代入¶
In [4]:
matrix_params = [(b_mat[0,0], 1), (b_mat[0,1], 1),
(Q_mat[0,0], 1), (Q_mat[0,1], -1),
(Q_mat[1,0], -1), (Q_mat[1,1], 2),
]
f_mat_with_param = f_mat.subs(matrix_params)[0].expand().simplify()
display(f_mat_with_param)
$$0.5 x_{00}^{2} - 1.0 x_{00} x_{10} + x_{00} + 1.0 x_{10}^{2} + x_{10}$$
jacobian,hessianを関数として作成¶
In [5]:
np_func = sy.lambdify(x_mat, f_mat_with_param, modules='numpy')
grad_func = grad(np_func) # return must be scalar
jacobian_vector = jacobian(np_func, 0) # return can take vector
hessian_matrix = hessian(np_func) # return can take vector
display(inspect.getsource(grad_func).split('\n'))
display(inspect.getsource(jacobian_vector).split('\n'))
display(inspect.getsource(hessian_matrix).split('\n'))
display(np_func, grad_func, jacobian_vector, hessian_matrix)
[' @wrap_nary_f(fun, unary_operator, argnum)',
' def nary_f(*args, **kwargs):',
' @wraps(fun)',
' def unary_f(x):',
' if isinstance(argnum, int):',
' subargs = subvals(args, [(argnum, x)])',
' else:',
' subargs = subvals(args, zip(argnum, x))',
' return fun(*subargs, **kwargs)',
' if isinstance(argnum, int):',
' x = args[argnum]',
' else:',
' x = tuple(args[i] for i in argnum)',
' return unary_operator(unary_f, x, *nary_op_args, **nary_op_kwargs)',
'']
[' @wrap_nary_f(fun, unary_operator, argnum)',
' def nary_f(*args, **kwargs):',
' @wraps(fun)',
' def unary_f(x):',
' if isinstance(argnum, int):',
' subargs = subvals(args, [(argnum, x)])',
' else:',
' subargs = subvals(args, zip(argnum, x))',
' return fun(*subargs, **kwargs)',
' if isinstance(argnum, int):',
' x = args[argnum]',
' else:',
' x = tuple(args[i] for i in argnum)',
' return unary_operator(unary_f, x, *nary_op_args, **nary_op_kwargs)',
'']
[' @wrap_nary_f(fun, unary_operator, argnum)',
' def nary_f(*args, **kwargs):',
' @wraps(fun)',
' def unary_f(x):',
' if isinstance(argnum, int):',
' subargs = subvals(args, [(argnum, x)])',
' else:',
' subargs = subvals(args, zip(argnum, x))',
' return fun(*subargs, **kwargs)',
' if isinstance(argnum, int):',
' x = args[argnum]',
' else:',
' x = tuple(args[i] for i in argnum)',
' return unary_operator(unary_f, x, *nary_op_args, **nary_op_kwargs)',
'']
<function numpy.<lambda>>
<function autograd.wrap_util.unary_to_nary.<locals>.nary_operator.<locals>.nary_f>
<function autograd.wrap_util.unary_to_nary.<locals>.nary_operator.<locals>.nary_f>
<function autograd.wrap_util.unary_to_nary.<locals>.nary_operator.<locals>.nary_f>
関数に具体的な引数を入れてグラフ化¶
並列化して値を取得する¶
関数¶
multiprocessing@Windowsは挙動怪しいためWSLで実行推奨
In [6]:
def calc_func(arg):
x1, x2 = arg
return [x1, x2, np_func(x1, x2)]
def calc_jacobian(arg):
x1, x2 = arg
return [x1, x2, jacobian_vector(x1, x2)]
def calc_hessian(arg):
x1, x2 = arg
return [x1, x2, hessian_matrix(x1, x2)]
def calc_parallel(func, x_lists, column_list):
df = pd.DataFrame(columns=column_list)
pool = mp.Pool(processes=mp.cpu_count() - 1)
tmp_df = pd.DataFrame(pool.map(func, x_lists), columns=column_list)
pool.close()
pool.join()
return df.append(tmp_df)
関数の実行¶
In [7]:
x_min = -10
x_max = 10
x_delta = 1
x_lists = [ (float(x1), float(x2))
for x1 in list(range(x_min, x_max, x_delta))
for x2 in list(range(x_min, x_max, x_delta))
]
column_list = ['x1', 'x2', 'y']
func_df = calc_parallel(calc_func, x_lists, column_list)
jacobian_df = calc_parallel(calc_jacobian, x_lists, column_list)
hessian_df = calc_parallel(calc_hessian, x_lists, column_list)
See https://github.com/HIPS/autograd/issues/84 for speeding up
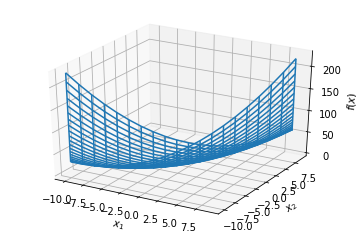
3D¶
f(x)¶
In [8]:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
func_pivot_df = func_df.pivot(index='x1', columns='x2', values='y')
x1_pivot = func_pivot_df.index.values
x2_pivot = func_pivot_df.columns.values
y_pivot = func_pivot_df.values
#ax.plot_surface(x1_pivot, x2_pivot, y_pivot, cmap='jet')
ax.plot_wireframe(x1_pivot, x2_pivot, y_pivot)
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('$f(x)$', rotation=90)
plt.show()
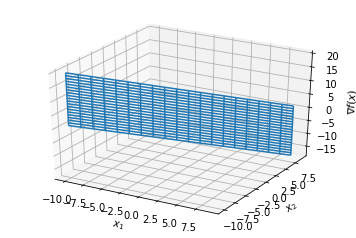
Jacobian¶
In [9]:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
jacobian_pivot_df = jacobian_df.pivot(index='x1', columns='x2', values='y')
j_x1_pivot = jacobian_pivot_df.index.values
j_x2_pivot = jacobian_pivot_df.columns.values
j_y_pivot = jacobian_pivot_df.values
ax.plot_wireframe(j_x1_pivot, j_x2_pivot, j_y_pivot)
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('$\\nabla f(x)$', rotation=90)
plt.show()
Where is Jacobian == 0 ?¶
In [10]:
#tmp_df = jacobian_df[(jacobian_df.y <= 10e-5) & (jacobian_df.y >= -10e-5)]
tmp_df = jacobian_df[jacobian_df.y == 0]
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
p = ax.scatter(tmp_df['x1'], tmp_df['x2'], tmp_df['y'], cmap=plt.hot())
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('$\\nabla f(x)$', rotation=90)
plt.show()
display(tmp_df)
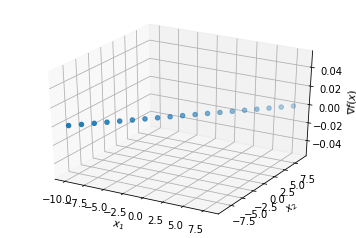
| x1 | x2 | y | |
|---|---|---|---|
| 1 | -10.0 | -9.0 | 0.0 |
| 22 | -9.0 | -8.0 | 0.0 |
| 43 | -8.0 | -7.0 | 0.0 |
| 64 | -7.0 | -6.0 | 0.0 |
| 85 | -6.0 | -5.0 | 0.0 |
| 106 | -5.0 | -4.0 | 0.0 |
| 127 | -4.0 | -3.0 | 0.0 |
| 148 | -3.0 | -2.0 | 0.0 |
| 169 | -2.0 | -1.0 | 0.0 |
| 190 | -1.0 | 0.0 | 0.0 |
| 211 | 0.0 | 1.0 | 0.0 |
| 232 | 1.0 | 2.0 | 0.0 |
| 253 | 2.0 | 3.0 | 0.0 |
| 274 | 3.0 | 4.0 | 0.0 |
| 295 | 4.0 | 5.0 | 0.0 |
| 316 | 5.0 | 6.0 | 0.0 |
| 337 | 6.0 | 7.0 | 0.0 |
| 358 | 7.0 | 8.0 | 0.0 |
| 379 | 8.0 | 9.0 | 0.0 |
Hessian¶
In [11]:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
hessian_pivot_df = hessian_df.pivot(index='x1', columns='x2', values='y')
h_x1_pivot = hessian_pivot_df.index.values
h_x2_pivot = hessian_pivot_df.columns.values
h_y_pivot = hessian_pivot_df.values
ax.plot_wireframe(h_x1_pivot, h_x2_pivot, h_y_pivot)
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('$\\nabla^2 f(x)$', rotation=90)
plt.show()