231 蒸気圧縮冷凍サイクル¶
読み込み¶
In [1]:
import numpy as np
import pandas as pd
import CoolProp.CoolProp as CP
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
パラメータ定義¶
In [2]:
WF = 'Ammonia'
K = 273.16 # converter from degC to K
T_C = -30 +K #freezer air temperature deg C
DT_evap = 5 # evaporator approach temperature difference K
DT_sh = 4 # degree of supergeat K
T_H = 30 +K# Outdoor air temperature degC
DT_cond = 10 # condenser approach temperature difference K
DT_sc = 4 # degree of subcooling K
ETA_c = 0.78 # compressor efficiency
V_dot_disp = 16.52*1e-3 # compressor displacement m^3/sec
ETA_vol = 0.75 # compressor volumetric efficiency
データフレーム用意¶
Nomenclature¶
| Symbol | Description | Unit |
|---|---|---|
| \(T\) | Temperature | \(K\) |
| \(P\) | Pressure | \(Pa\) |
| \(s\) | Specific entropy | \(J/kg-K\) |
| \(v\) | Specific volume | \(m^3/kg\) |
| \(h\) | Specific enthalpy | \(J/kg\) |
| \(h_s\) | Specific enthalpy leaving reversible process | \(J/kg\) |
In [3]:
states = pd.DataFrame(columns=['T', 'P', 's', 'v', 'h', 'h_s'], index=list(range(1,4+1)))
State 4¶
\begin{align}
T_4 = T_H + \Delta T_{cond} \\
T_{cond} = T_4 + \Delta T_{sc}
\end{align}
In [4]:
states.loc[4, 'T'] = T_H + DT_cond
T_cond = states.loc[4, 'T'] + DT_sc
states.loc[4, 'P'] = CP.PropsSI('P', 'T', T_cond, 'Q', 0, WF)
states.loc[4, 's'] = CP.PropsSI('S', 'T', states.loc[4, 'T'], 'P', states.loc[4, 'P'], WF)
states.loc[4, 'h'] = CP.PropsSI('H', 'T', states.loc[4, 'T'], 'P', states.loc[4, 'P'], WF)
State 2¶
\begin{align}
T_2 = T_C - \Delta T_{evap} \\
T_{evap} = T_2 - \Delta T_{sh}
\end{align}
In [5]:
states.loc[2, 'T'] = T_C - DT_evap
T_evap = states.loc[2, 'T'] - DT_sh
states.loc[2, 'P'] = CP.PropsSI('P', 'T', T_evap, 'Q', 1, WF)
states.loc[2, 's'] = CP.PropsSI('S', 'T', states.loc[2, 'T'], 'P', states.loc[2, 'P'], WF)
states.loc[2, 'h'] = CP.PropsSI('H', 'T', states.loc[2, 'T'], 'P', states.loc[2, 'P'], WF)
states.loc[2, 'v'] = 1/CP.PropsSI('D', 'T', states.loc[2, 'T'], 'P', states.loc[2, 'P'], WF)
State 3¶
\begin{align}
\frac{\dot{W}_{s,c}}{\dot{m}} = h_{s,3} - h_2 \\
\frac{\dot{W}_c}{\dot{m}} = \frac{1}{\eta_c}\frac{\dot{W}_{s,c}}{\dot{m}} \\
h_3 = h_2 + \frac{\dot{W}_c}{\dot{m}}
\end{align}
In [6]:
states.loc[3, 'P'] = states.loc[4, 'P']
states.loc[3, 'h_s'] = CP.PropsSI('H', 'P', states.loc[3, 'P'], 'S', states.loc[2, 's'], WF)
W_dot_s_c_m_dot = states.loc[3, 'h_s'] - states.loc[2, 'h']
W_dot_c_m_dot = W_dot_s_c_m_dot/ETA_c
states.loc[3, 'h'] = states.loc[2, 'h'] + W_dot_c_m_dot
states.loc[3, 's'] = CP.PropsSI('S', 'P', states.loc[3, 'P'], 'H', states.loc[3, 'h'], WF)
states.loc[3, 'T'] = CP.PropsSI('T', 'P', states.loc[3, 'P'], 'H', states.loc[3, 'h'], WF)
State 1¶
\begin{align}
P_1 = P_2 \\
h_1 = h_4
\end{align}
In [7]:
states.loc[1, 'P'] = states.loc[2, 'P']
states.loc[1, 'h'] = states.loc[4, 'h']
states.loc[1, 's'] = CP.PropsSI('S', 'P', states.loc[1, 'P'], 'H', states.loc[1, 'h'], WF)
states.loc[1, 'T'] = CP.PropsSI('T', 'P', states.loc[1, 'P'], 'H', states.loc[1, 'h'], WF)
In [8]:
states
Out[8]:
| T | P | s | v | h | h_s | |
|---|---|---|---|---|---|---|
| 1 | 234.16 | 75654.7 | 2345.06 | NaN | 533872 | NaN |
| 2 | 238.16 | 75654.7 | 6733.31 | 1.50504 | 1.5615e+06 | NaN |
| 3 | 537.516 | 1.7358e+06 | 7021.6 | NaN | 2.22854e+06 | 2.08179e+06 |
| 4 | 313.16 | 1.7358e+06 | 2115.4 | NaN | 533872 | NaN |
飽和蒸気曲線の作成¶
In [9]:
P_list = list(range(int(7*1e+3), int(11.3*1e+6), int(1e+3)))
saturation_curve = {}
saturation_curve['Ts'] = {'s':[], 'T':[]}
for P in P_list:
saturation_curve['Ts']['T'].append(CP.PropsSI('T', 'P', P, 'Q', 0, WF))
saturation_curve['Ts']['s'].append(CP.PropsSI('S', 'P', P, 'Q', 0, WF))
for P in P_list[::-1]:
saturation_curve['Ts']['T'].append(CP.PropsSI('T', 'P', P, 'Q', 1, WF))
saturation_curve['Ts']['s'].append(CP.PropsSI('S', 'P', P, 'Q', 1, WF))
saturation_curve['ph'] = {'p':[], 'h':[]}
T_list = list(range(196, 405))
for T in T_list:
saturation_curve['ph']['p'].append(CP.PropsSI('P', 'T', T, 'Q', 0, WF))
saturation_curve['ph']['h'].append(CP.PropsSI('H', 'T', T, 'Q', 0, WF)/1e6)
for T in T_list[::-1]:
saturation_curve['ph']['p'].append(CP.PropsSI('P', 'T', T, 'Q', 1, WF))
saturation_curve['ph']['h'].append(CP.PropsSI('H', 'T', T, 'Q', 1, WF)/1e6)
Chart¶
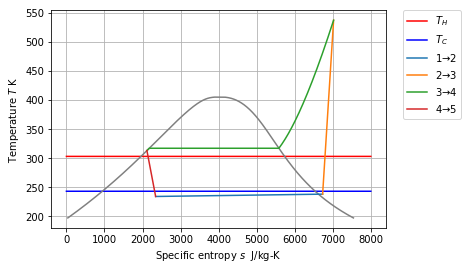
T-s¶
In [10]:
s_max = 8000
s_list = range(0, s_max)
plt.plot(s_list, [T_H]*s_max, label='$T_H$', color='red')
plt.plot(s_list, [T_C]*s_max, label='$T_C$', color='blue')
plt.plot(saturation_curve['Ts']['s'], saturation_curve['Ts']['T'], color='gray')
nb_points = 1000
s12 = np.linspace(states.loc[1, 's'], states.loc[2, 's'], nb_points)
s23 = np.linspace(states.loc[2, 's'], states.loc[3, 's'], nb_points)
s34 = np.linspace(states.loc[3, 's'], states.loc[4, 's'], nb_points)
s41 = np.linspace(states.loc[4, 's'], states.loc[1, 's'], nb_points)
T12 = np.linspace(states.loc[1, 'T'], states.loc[2, 'T'], nb_points)
T23 = np.linspace(states.loc[2, 'T'], states.loc[3, 'T'], nb_points)
T34 = []
for s in s34:
T34.append(CP.PropsSI('T', 'S', s, 'P', states.loc[3, 'P'], WF))
T41 = np.linspace(states.loc[4, 'T'], states.loc[1, 'T'], nb_points)
L_T = [T12, T23, T34, T41]
L_s = [s12, s23, s34, s41]
for i in range(len(L_s)):
plt.plot(L_s[i],L_T[i],label='{}$\\to${}'.format(i+1,(i+1)%5+1))
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0)
plt.xlabel('Specific entropy $s$ J/kg-K')
plt.ylabel('Temperature $T$ K')
plt.grid()
plt.show()
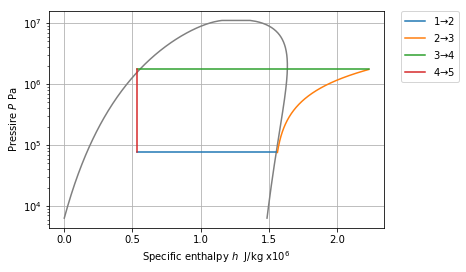
P-h¶
In [11]:
plt.plot(saturation_curve['ph']['h'], saturation_curve['ph']['p'], color='gray')
nb_points = 1000
h12 = np.linspace(states.loc[1, 'h'], states.loc[2, 'h'], nb_points)
h23 = np.linspace(states.loc[2, 'h'], states.loc[3, 'h'], nb_points)
h34 = np.linspace(states.loc[3, 'h'], states.loc[4, 'h'], nb_points)
h41 = np.linspace(states.loc[4, 'h'], states.loc[1, 'h'], nb_points)
P12 = np.linspace(states.loc[1, 'P'], states.loc[2, 'P'], nb_points)
P23 = np.linspace(states.loc[2, 'P'], states.loc[3, 'P'], nb_points)
P34 = np.linspace(states.loc[3, 'P'], states.loc[4, 'P'], nb_points)
P41 = np.linspace(states.loc[4, 'P'], states.loc[1, 'P'], nb_points)
L_h = [h12, h23, h34, h41]
L_P = [P12, P23, P34, P41]
for i in range(len(L_h)):
plt.plot(L_h[i]/1e6, L_P[i],label='{}$\\to${}'.format(i+1,(i+1)%5+1))
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0)
plt.xlabel("Specific enthalpy $h$ J/kg x$10^6$")
plt.ylabel('Pressire $P$ Pa')
plt.yscale("log")
plt.grid()
plt.show()
Perfoemance of regrigeration cycle¶
\begin{align}
\dot{m} = \frac{\dot{V}_{disp}\eta_{vol}}{v_2} \\
\dot{W}_c = \dot{m}(h_3-h_2) \\
\dot{Q}_{evap} = \dot{m}(h_2-h_1) \\
\dot{Q}_{cond} = \dot{m}(h_3-h_4) \\
COP = \frac{\dot{Q}_{evap}}{\dot{W}_c}
\end{align}
In [12]:
m_dot = V_dot_disp*ETA_vol/states.loc[2, 'v']
W_dot_c = m_dot*(states.loc[3, 'h'] - states.loc[2, 'h'])
Q_dot_evap = m_dot*(states.loc[2, 'h']-states.loc[1, 'h'])
Q_dot_cond = m_dot*(states.loc[3, 'h'] -states.loc[4, 'h'])
COP = Q_dot_evap/W_dot_c
display(m_dot, W_dot_c, Q_dot_evap, Q_dot_cond, COP)
0.00823235241270052
5491.324347983485
8459.801237460124
13951.12558544361
1.540575770317905
Freezer design¶
\begin{align}
{COST}_c = 92\times 10^5 [JPY-s/m^3] \dot{V}_{disp} \\
{COST}_{cond} = 1.5\times 10^2 [JPY-K/W] UA_{cond} \\
{COST}_{evap} = 1.25\times 10^2 [JPY-K/W] UA_{evap} \\
UA_{cond} = \frac{\dot{Q}_{cond}}{(T_{cond}-T_H)} \\
UA_{evap} = \frac{\dot{Q}_{evap}}{(T_C-T_{evap})}
\end{align}
In [13]:
COST_c = 92e5*V_dot_disp
UA_cond = Q_dot_cond/(T_cond - T_H)
UA_evap = Q_dot_evap/(T_C - T_evap)
COST_cond = 1.5e2*UA_cond
COST_evap = 1.25e2*UA_evap
COST_system = COST_c + COST_cond + COST_evap
\begin{equation}
COST_{operating} = ec\dot{W}_{c} time
\end{equation}
In [14]:
ec = 10 # JPY/kWh
time = 5 *8760 #year
COST_operating = ec*W_dot_c/1000 *time
In [15]:
COST_total = COST_system+COST_operating
display(COST_total, COST_system, COST_operating)
2824157.649384259
418957.58496749273
2405200.064416766