121 代数計算機による常微分方程式の解法

読み込み

import sympy as sy
sy.init_printing(use_latex=True)

import matplotlib.pyplot as plt
%matplotlib inline

import warnings
warnings.filterwarnings("ignore")

変数定義

\begin{align} m\ddot{x}+c\dot{x}+kx &= f(t) \\ LC\frac{d^2v_o}{dt^2}+RC\frac{dv_o}{dt}+v_o(t) &= v_i(t) \end{align}

t = sy.Symbol('t', real=True)

# バネマスダンパ系
x, f = sy.symbols('x, f', real=True)
m, c, k = sy.symbols('m c k', real=True, positive=True)
mech_eq = sy.Eq(m*x(t).diff(t,2)+c*x(t).diff(t,1)+k*x(t), f(t))

#LRC直列回路
v_o, v_i = sy.symbols('v_o v_i')
L, R, C = sy.symbols('L R C', real=True, positive=True)
LRC_eq = sy.Eq(L*C*v_o(t).diff(t,2)+R*C*v_o(t).diff(t,1)+v_o(t), v_i(t))

display(mech_eq, LRC_eq)

$$c \frac{d}{d t} x{\left (t \right )} + k x{\left (t \right )} + m \frac{d^{2}}{d t^{2}} x{\left (t \right )} = f{\left (t \right )}$$

$$C L \frac{d^{2}}{d t^{2}} \operatorname{v_{o}}{\left (t \right )} + C R \frac{d}{d t} \operatorname{v_{o}}{\left (t \right )} + \operatorname{v_{o}}{\left (t \right )} = \operatorname{v_{i}}{\left (t \right )}$$

一般解

#理解を助けるため左辺のみ考え斉次とする
mech_gen_ans = sy.dsolve(mech_eq.lhs)
LRC_gen_ans = sy.dsolve(LRC_eq.lhs)

display(mech_gen_ans, LRC_gen_ans)

$$x{\left (t \right )} = C_{1} e^{\frac{t}{2 m} \left(- c - \sqrt{c^{2} - 4 k m}\right)} + C_{2} e^{\frac{t}{2 m} \left(- c + \sqrt{c^{2} - 4 k m}\right)}$$

$$\operatorname{v_{o}}{\left (t \right )} = C_{1} e^{\frac{t}{2 L} \left(- R - \frac{1}{\sqrt{C}} \sqrt{C R^{2} - 4 L}\right)} + C_{2} e^{\frac{t}{2 L} \left(- R + \frac{1}{\sqrt{C}} \sqrt{C R^{2} - 4 L}\right)}$$

特殊解

初期条件の設定

x_0, d_x_0 = sy.symbols('x_0 \dot{x}_0', real=True)
mech_init_condition = sy.Eq(mech_gen_ans.rhs.subs(t, 0), x_0) #x(0) = x_0
mech_init_condition_dot = sy.Eq(mech_gen_ans.rhs.diff(t).subs(t, 0), d_x_0) #\dot{x}(0) = d_x_0

v_o0, d_v_o0 = sy.symbols('v_o0 \dot{v}_{o0}', real=True)
LRC_init_condition = sy.Eq(LRC_gen_ans.rhs.subs(t, 0), v_o0) #v_o(0) = v_o0
LRC_init_condition_dot = sy.Eq(LRC_gen_ans.rhs.diff(t).subs(t, 0), d_v_o0) #\dot{v}_o(0) = d_v_0

display(mech_init_condition, mech_init_condition_dot, LRC_init_condition, LRC_init_condition_dot)

$$C_{1} + C_{2} = x_{0}$$

$$\frac{C_{1}}{2 m} \left(- c - \sqrt{c^{2} - 4 k m}\right) + \frac{C_{2}}{2 m} \left(- c + \sqrt{c^{2} - 4 k m}\right) = \dot{x}_0$$

$$C_{1} + C_{2} = v_{o0}$$

$$\frac{C_{1}}{2 L} \left(- R - \frac{1}{\sqrt{C}} \sqrt{C R^{2} - 4 L}\right) + \frac{C_{2}}{2 L} \left(- R + \frac{1}{\sqrt{C}} \sqrt{C R^{2} - 4 L}\right) = \dot{v}_{o0}$$

積分定数について解く

C1, C2 = sy.symbols('C1, C2')
mech_C1C2_solution = sy.solve([mech_init_condition, mech_init_condition_dot], [C1, C2])
LRC_C1C2_solution = sy.solve([LRC_init_condition, LRC_init_condition_dot], [C1, C2])

display(mech_C1C2_solution, LRC_C1C2_solution)

$$\left \{ C_{1} : \frac{1}{\sqrt{c^{2} - 4 k m}} \left(- \dot{x}_0 m - \frac{c x_{0}}{2} + \frac{x_{0}}{2} \sqrt{c^{2} - 4 k m}\right), \quad C_{2} : \frac{1}{\sqrt{c^{2} - 4 k m}} \left(\dot{x}_0 m + \frac{x_{0}}{2} \left(c + \sqrt{c^{2} - 4 k m}\right)\right)\right \}$$

$$\left \{ C_{1} : \frac{1}{\sqrt{C R^{2} - 4 L}} \left(- \sqrt{C} L \dot{v}_{o0} - \frac{R v_{o0}}{2} \sqrt{C} + \frac{v_{o0}}{2} \sqrt{C R^{2} - 4 L}\right), \quad C_{2} : \frac{1}{\sqrt{C R^{2} - 4 L}} \left(\sqrt{C} L \dot{v}_{o0} + \frac{v_{o0}}{2} \left(\sqrt{C} R + \sqrt{C R^{2} - 4 L}\right)\right)\right \}$$

積分定数を戻す

mech_special_ans = mech_gen_ans.subs(mech_C1C2_solution)
LRC_special_ans = LRC_gen_ans.subs(LRC_C1C2_solution)

display(mech_special_ans.simplify(), LRC_special_ans.simplify())

$$x{\left (t \right )} = \frac{e^{- \frac{c t}{m}}}{2 \sqrt{c^{2} - 4 k m}} \left(\left(2 \dot{x}_0 m + x_{0} \left(c + \sqrt{c^{2} - 4 k m}\right)\right) e^{\frac{t}{2 m} \left(c + \sqrt{c^{2} - 4 k m}\right)} + \left(- 2 \dot{x}_0 m - c x_{0} + x_{0} \sqrt{c^{2} - 4 k m}\right) e^{\frac{t}{2 m} \left(c - \sqrt{c^{2} - 4 k m}\right)}\right)$$

$$\operatorname{v_{o}}{\left (t \right )} = \frac{e^{- \frac{R t}{L}}}{2 \sqrt{C R^{2} - 4 L}} \left(\left(2 \sqrt{C} L \dot{v}_{o0} + v_{o0} \left(\sqrt{C} R + \sqrt{C R^{2} - 4 L}\right)\right) e^{\frac{t}{2 \sqrt{C} L} \left(\sqrt{C} R + \sqrt{C R^{2} - 4 L}\right)} + \left(- 2 \sqrt{C} L \dot{v}_{o0} - \sqrt{C} R v_{o0} + v_{o0} \sqrt{C R^{2} - 4 L}\right) e^{\frac{t}{2 \sqrt{C} L} \left(\sqrt{C} R - \sqrt{C R^{2} - 4 L}\right)}\right)$$

パラメータ代入

def round_sympyeq(eq, digit):
    eq_rounded = eq
    for value in sy.preorder_traversal(eq):
        if value.is_number:
            eq_rounded = eq_rounded.subs(value, round(value, digit))
    return eq_rounded

mech_params = [(m, 0.5), (c, 3.5), (k, 2.5), (x_0, 1), (d_x_0, 0)]
#mech_param_dict = {m:0.5, c:3.5, k:2.5, x_0:0, d_x_0:0} # for evalf(subs=args)
mech_special_ans_specified = mech_gen_ans.subs(mech_params)\
                                    .subs(sy.solve([mech_init_condition.subs(mech_params),
                                                    mech_init_condition_dot.subs(mech_params)],
                                                   [C1, C2]))
mech_ans_rounded = round_sympyeq(mech_special_ans_specified, 3)

LRC_params = [(L, 0.5),(R, 3.5), (C, 2.5), (v_o0, 1), (d_v_o0, 0)]
LRC_special_ans_specified = LRC_gen_ans.subs(LRC_params)\
                                    .subs(sy.solve([LRC_init_condition.subs(LRC_params),
                                                    LRC_init_condition_dot.subs(LRC_params)],
                                                   [C1, C2]))
LRC_ans_rounded = round_sympyeq(LRC_special_ans_specified, 3)

display(mech_ans_rounded)
display(LRC_ans_rounded)

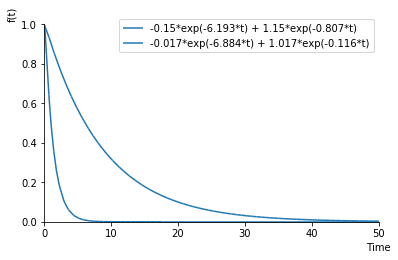
$$x{\left (t \right )} = - 0.15 e^{- 6.193 t} + 1.15 e^{- 0.807 t}$$

$$\operatorname{v_{o}}{\left (t \right )} = - 0.017 e^{- 6.884 t} + 1.017 e^{- 0.116 t}$$

グラフ化

sy.plot(mech_ans_rounded.rhs, LRC_ans_rounded.rhs, (t, 0, 50), xlabel='Time',legend=True)

<sympy.plotting.plot.Plot at 0x7fa474d670b8>