241 暖房向け自然冷媒ヒートポンプサイクル¶

読み込み¶

In [1]:

import numpy as np
import pandas as pd

import CoolProp.CoolProp as CP

import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")

パラメータ定義¶

汎用¶

In [2]:

K = 273.16 # converter from degC to K

外生条件¶

In [3]:

params = {
'WF':'CarbonDioxide', # working fluid
'T_bldg': 20 +K, #freezer air temperature degC
'T_amb': -5 +K,   # Outdoor air temperature degC

'DT_cond':5,   # condenser approach temperature difference K
'DT_sc':3,      # degree of subcooling K
'DT_evap':4,     # evaporator approach temprature difference K
'DT_sh':2,      # degree of superheat K

'V_dot_cond_f':2.0, # condenser fan volumetric flow rate m3/s
'V_dot_evap_f':2.5, # evaporator fan volumetric flow rate m3/s

'W_dot_cond_f':200, # condenser fan power W
'W_dot_evap_f':300, # evaporator fan power W

'ETA_cond':0.72, # condenser effectiveness
'ETA_evap':0.81, # evaporator effectiveness

'c':0.025,      # clearance volume rate
'V_dot_disp':2*1e-3, # compressor displacement m^3/sec
}

データフレーム用意¶

Nomenclature¶

Symbol	Description	Unit
\(T\)	Temperature	\(K\)
\(P\)	Pressure	\(Pa\)
\(s\)	Specific entropy	\(J/kg-K\)
\(s_s\)	Specific entropy leaving reversible process	\(J/kg-K\)
\(v\)	Specific volume	\(m^3/kg\)
\(h\)	Specific enthalpy	\(J/kg\)
\(h_s\)	Specific enthalpy leaving reversible process	\(J/kg\)

In [4]:

states = pd.DataFrame(columns=['T', 'P', 's', 's_s', 'v', 'h', 'h_s'],
                      index=list(range(1,4+1)))

State 4¶

\begin{align} State4 =& f(T_{cond}, x_4=0) \\ \rm{where} & \\ T_4 =& T_{bldg} + \Delta T_{cond}, \\ T_{cond} =& T_4 + \Delta T_{sc}. \end{align}

In [5]:

states.loc[4, 'T'] = params['T_bldg'] + params['DT_cond']
T_cond = states.loc[4, 'T'] + params['DT_sc']
states.loc[4, 'P'] = CP.PropsSI('P', 'T', T_cond, 'Q', 0, params['WF']) # Satuation pressure
states.loc[4, 's'] = CP.PropsSI('S', 'T', states.loc[4, 'T'],
                                     'P', states.loc[4, 'P'], params['WF'])
states.loc[4, 'h'] = CP.PropsSI('H', 'T', states.loc[4, 'T'],
                                     'P', states.loc[4, 'P'], params['WF'])
ax = plt.axes([0,0,0,0])
ax.axis('off')
plt.text(0, 0, "$T_{cond}$="+'{:.02f} K'.format(T_cond), size=14)
plt.show()

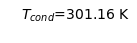
../_images/materials_241_heat_pump_system_9_0.png

State 2¶

\begin{align} State2 =& f(T_{evap}, x_2=1) \\ \rm{where} & \\ T_2 =& T_{amb} - \Delta T_{evap}, \\ T_{evap} =& T_2 - \Delta T_{sh}. \end{align}

In [6]:

states.loc[2, 'T'] = params['T_amb'] - params['DT_evap']
T_evap = states.loc[2, 'T'] - params['DT_sh']
states.loc[2, 'P'] = CP.PropsSI('P', 'T', T_evap, 'Q', 1, params['WF']) # Satuation pressure
states.loc[2, 's'] = CP.PropsSI('S', 'T', states.loc[2, 'T'],
                                     'P', states.loc[2, 'P'], params['WF'])
states.loc[2, 'h'] = CP.PropsSI('H', 'T', states.loc[2, 'T'],
                                     'P', states.loc[2, 'P'], params['WF'])
states.loc[2, 'v'] = 1/CP.PropsSI('D', 'T', states.loc[2, 'T'],
                                       'P', states.loc[2, 'P'], params['WF'])
ax = plt.axes([0,0,0,0])
ax.axis('off')
plt.text(0, 0, "$T_{evap}$="+'{:.02f} K'.format(T_evap), size=14)
plt.show()

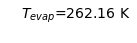
../_images/materials_241_heat_pump_system_11_0.png

State 1¶

\begin{align} State1 =& f(P_1, h_1) \\ \rm{where} \\ P_1 =& P_2 \text{ which means that pressure loss in the evaporator is neglected,} \\ h_1 =& h_4 \text{ which means that the valve is isenthalpic.} \end{align}

In [7]:

states.loc[1, 'P'] = states.loc[2, 'P']
states.loc[1, 'h'] = states.loc[4, 'h']
states.loc[1, 's'] = CP.PropsSI('S', 'P', states.loc[1, 'P'],
                                     'H', states.loc[1, 'h'], params['WF'])
states.loc[1, 'T'] = CP.PropsSI('T', 'P', states.loc[1, 'P'],
                                     'H', states.loc[1, 'h'], params['WF'])

State 3¶

\begin{align} State3 =& f(P_3, h_3, ) \\ \rm{where} \\ P_3 =& P_4 \text{ which means that pressure loss in the condenser is neglected,} \\ \frac{\dot{W}_{s,c}}{\dot{m}} =& h_{s,3} -h_2 \\ \frac{\dot{W}_{c}}{\dot{m}} =& \frac{1}{\eta_c}\frac{\dot{W}_{s,c}}{\dot{m}}\\ h_3 =& h_2+\frac{\dot{W}_{c}}{\dot{m}} \end{align}

In [8]:

states.loc[3, 'P'] = states.loc[4, 'P']
eta_c = 0.79 - 0.0074*(T_cond - T_evap)
states.loc[3, 's_s'] = states.loc[2, 's'] # specific entropy leaving isentropic compressor
states.loc[3, 'h_s'] = CP.PropsSI('H', 'P', states.loc[3, 'P'],
                                       'S', states.loc[3, 's_s'], params['WF']) # specific enthalpy leaving isentropic compressor
W_dot_s_c_m_dot = states.loc[3, 'h_s'] - states.loc[2, 'h']
W_dot_c_m_dot = W_dot_s_c_m_dot/eta_c
states.loc[3, 'h'] = states.loc[2, 'h'] + W_dot_c_m_dot
states.loc[3, 's'] = CP.PropsSI('S', 'P', states.loc[3, 'P'],
                                     'H', states.loc[3, 'h'], params['WF'])
states.loc[3, 'T'] = CP.PropsSI('T', 'P', states.loc[3, 'P'],
                                     'H', states.loc[3, 'h'], params['WF'])
states.loc[3, 'v'] = 1/CP.PropsSI('D', 'P', states.loc[3, 'P'],
                                     'H', states.loc[3, 'h'], params['WF'])

In [9]:

ax = plt.axes([0,0,0,0.1])
ax.axis('off')
plt.text(0, 1.0, "$\eta_{c}$="+'{:.02f}'.format(eta_c), size=14)
plt.text(0, 0.5, "$\dot{W}_{s,c}/\dot{m}$="+'{:.02f} J/kg'.format(W_dot_s_c_m_dot), size=14)
plt.text(0, 0, "$\dot{W}_{c}/\dot{m}$="+'{:.02f} J/kg'.format(W_dot_s_c_m_dot), size=14)
plt.show()
display(states)

../_images/materials_241_heat_pump_system_16_0.png

	T	P	s	s_s	v	h	h_s
1	262.16	2.57478e+06	1271.96	NaN	NaN	269834	NaN
2	264.16	2.57478e+06	1914.6	NaN	0.0147807	438320	NaN
3	367.845	6.89339e+06	2032.34	1914.6	0.00827627	521470	480011
4	298.16	6.89339e+06	1229.75	NaN	NaN	269834	NaN

飽和蒸気曲線の作成¶

In [10]:

P_list = list(range(int(5.2*1e+5), int(7.377*1e+6), int(1e+3)))
saturation_curve = {}
saturation_curve['Ts'] = {'s':[], 'T':[]}
for P in P_list:
    saturation_curve['Ts']['T'].append(CP.PropsSI('T', 'P', P, 'Q', 0, params['WF']))
    saturation_curve['Ts']['s'].append(CP.PropsSI('S', 'P', P, 'Q', 0, params['WF']))
for P in P_list[::-1]:
    saturation_curve['Ts']['T'].append(CP.PropsSI('T', 'P', P, 'Q', 1, params['WF']))
    saturation_curve['Ts']['s'].append(CP.PropsSI('S', 'P', P, 'Q', 1, params['WF']))

saturation_curve['ph'] = {'p':[], 'h':[]}
T_list = list(range(217, 304))
for T in T_list:
    saturation_curve['ph']['p'].append(CP.PropsSI('P', 'T', T, 'Q', 0, params['WF'])/1e6)
    saturation_curve['ph']['h'].append(CP.PropsSI('H', 'T', T, 'Q', 0, params['WF'])/1e6)
for T in T_list[::-1]:
    saturation_curve['ph']['p'].append(CP.PropsSI('P', 'T', T, 'Q', 1, params['WF'])/1e6)
    saturation_curve['ph']['h'].append(CP.PropsSI('H', 'T', T, 'Q', 1, params['WF'])/1e6)

Chart¶

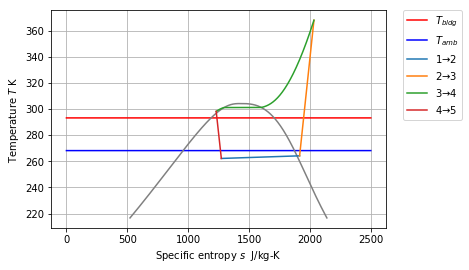
T-s¶

In [11]:

s_max = 2500
s_list = range(0, s_max)
plt.plot(s_list, [params['T_bldg']]*s_max, label='$T_{bldg}$', color='red')
plt.plot(s_list, [params['T_amb']]*s_max, label='$T_{amb}$', color='blue')
plt.plot(saturation_curve['Ts']['s'], saturation_curve['Ts']['T'], color='gray')

nb_points = 1000
s12 = np.linspace(states.loc[1, 's'], states.loc[2, 's'], nb_points)
s23 = np.linspace(states.loc[2, 's'], states.loc[3, 's'], nb_points)
s34 = np.linspace(states.loc[3, 's'], states.loc[4, 's'], nb_points)
s41 = np.linspace(states.loc[4, 's'], states.loc[1, 's'], nb_points)

T12 = np.linspace(states.loc[1, 'T'], states.loc[2, 'T'], nb_points)
T23 = np.linspace(states.loc[2, 'T'], states.loc[3, 'T'], nb_points)
T34 = []
for s in s34:
    T34.append(CP.PropsSI('T', 'S', s, 'P', states.loc[3, 'P'], params['WF']))
T41 = np.linspace(states.loc[4, 'T'], states.loc[1, 'T'], nb_points)

L_T = [T12, T23, T34, T41]
L_s = [s12, s23, s34, s41]

for i in range(len(L_s)):
    plt.plot(L_s[i],L_T[i],label='{}$\\to${}'.format(i+1,(i+1)%5+1))

plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0)
plt.xlabel('Specific entropy $s$  J/kg-K')
plt.ylabel('Temperature $T$ K')
plt.grid()
plt.show()

../_images/materials_241_heat_pump_system_20_0.png

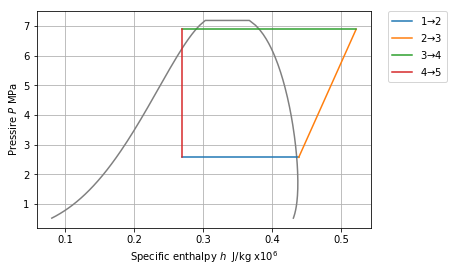
P-h¶

In [12]:

plt.plot(saturation_curve['ph']['h'], saturation_curve['ph']['p'], color='gray')

nb_points = 1000
h12 = np.linspace(states.loc[1, 'h'], states.loc[2, 'h'], nb_points)
h23 = np.linspace(states.loc[2, 'h'], states.loc[3, 'h'], nb_points)
h34 = np.linspace(states.loc[3, 'h'], states.loc[4, 'h'], nb_points)
h41 = np.linspace(states.loc[4, 'h'], states.loc[1, 'h'], nb_points)

P12 = np.linspace(states.loc[1, 'P'], states.loc[2, 'P'], nb_points)
P23 = np.linspace(states.loc[2, 'P'], states.loc[3, 'P'], nb_points)
P34 = np.linspace(states.loc[3, 'P'], states.loc[4, 'P'], nb_points)
P41 = np.linspace(states.loc[4, 'P'], states.loc[1, 'P'], nb_points)

L_h = [h12, h23, h34, h41]
L_P = [P12, P23, P34, P41]

for i in range(len(L_h)):
    plt.plot(L_h[i]/1e6, L_P[i]/1e6,label='{}$\\to${}'.format(i+1,(i+1)%5+1))

plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0)
plt.xlabel("Specific enthalpy $h$  J/kg x$10^6$")
plt.ylabel('Pressire $P$ MPa')
#plt.yscale("log")
plt.grid()
plt.show()

../_images/materials_241_heat_pump_system_22_0.png

Perfoemance of heat pump cycle¶

Power required by the compressor¶

\begin{align} \eta_{vol} = 1-c(\frac{v_2}{v_3}-1) \\ \dot{m} = \frac{\dot{V}_{disp}\eta_{vol}}{v_2} \\ \dot{W}_c = \frac{\dot{W}_c}{\dot{m}}\dot{m} \\ \end{align}

In [13]:

eta_vol = 1- params['c']*(states.loc[2, 'v']/states.loc[3, 'v'] - 1)
m_dot = params['V_dot_disp']*eta_vol/states.loc[2, 'v']
W_dot_c = W_dot_c_m_dot*m_dot

ax = plt.axes([0,0,0,0.2])
ax.axis('off')
plt.text(0, 1, "$\eta_{vol}$="+'{:.02f}'.format(eta_vol), size=14)
plt.text(0, 0.5, "$\dot{m}$="+'{:.02f} kg/s'.format(m_dot), size=14)
plt.text(0, 0, "$\dot{W}_{c}$="+'{:.02f} kW'.format(W_dot_c/1e3), size=14)
plt.show()

../_images/materials_241_heat_pump_system_24_0.png

Condenser heat transfer rate¶

\begin{align} \dot{Q}_{cond} = \dot{m}(h_3-h_4) \text{ or } \eta_{cond}\dot{m}_{a,cond}c_{p,a,cond}(T_{cond}-T_{bldg}) \\ \dot{m}_{a,cond} = \frac{\dot{V}_{cond,f}}{v_{a,cond}} \end{align}

In [14]:

Q_dot_cond = m_dot*(states.loc[3, 'h'] -states.loc[4, 'h'])
cP_a_cond = CP.PropsSI('Cp0mass', 'T', params['T_bldg'], 'P', 101325, 'Air')
v_a_cond = 1/CP.PropsSI('D', 'T', params['T_bldg'], 'P', 101325, 'Air')
m_dot_a_cond = params['V_dot_cond_f'] / v_a_cond

Q_dot_cond_alt = params['ETA_cond']*m_dot_a_cond*cP_a_cond*(T_cond - params['T_bldg'])

ax = plt.axes([0,0,0,0.3])
ax.axis('off')
plt.text(0, 1.0, "$\dot{Q}_{cond}$="+'{:.02f} kW'.format(Q_dot_cond/1e3), size=14)
plt.text(0, 0.75, "$\dot{Q}_{cond}^{alt}$="+'{:.02f} kW'.format(Q_dot_cond_alt/1e3), size=14)
plt.text(0, 0.5, "$\dot{c}_{p,a,cond}$="+'{:.02f} kJ/kg/K'.format(cP_a_cond/1e3), size=14)
plt.text(0, 0.25, "$v_{a,cond}$="+'{:.02f} $m^3$/kg'.format(v_a_cond), size=14)
plt.text(0, 0.0, "$\dot{m}_{a,cond}$="+'{:.02f} kg/s'.format(m_dot_a_cond), size=14)
plt.show()

../_images/materials_241_heat_pump_system_26_0.png

Evaporator heat transfer rate¶

\begin{align} \dot{Q}_{evap} = \dot{m}(h_2-h_1) \text{ or } \eta_{evap}\dot{m}_{a,evap}c_{p,a,evap}(T_{amb}-T_{evap}) \\ \dot{m}_{a,evap} = \frac{\dot{V}_{evap,f}}{v_{a,evap}} \end{align}

In [15]:

Q_dot_evap = m_dot*(states.loc[2, 'h']-states.loc[1, 'h'])
cP_a_evap = CP.PropsSI('Cp0mass', 'T', params['T_amb'], 'P', 101325, 'Air')
v_a_evap = 1/CP.PropsSI('D', 'T', params['T_amb'], 'P', 101325, 'Air')
m_dot_a_evap = params['V_dot_evap_f'] / v_a_evap

Q_dot_evap_alt = params['ETA_evap']*m_dot_a_evap*cP_a_evap*(params['T_amb'] - T_evap)

ax = plt.axes([0,0,0,0.3])
ax.axis('off')
plt.text(0, 1.0, "$\dot{Q}_{evap}$="+'{:.02f} kW'.format(Q_dot_evap/1e3), size=14)
plt.text(0, 0.75, "$\dot{Q}_{evap}^{alt}$="+'{:.02f} kW'.format(Q_dot_evap_alt/1e3), size=14)
plt.text(0, 0.5, "$\dot{c}_{p,a,evap}$="+'{:.02f} kJ/kg/K'.format(cP_a_evap/1e3), size=14)
plt.text(0, 0.25, "$v_{a,evap}$="+'{:.02f} $m^3$/kg'.format(v_a_evap), size=14)
plt.text(0, 0.0, "$\dot{m}_{a,evap}$="+'{:.02f} kg/s'.format(m_dot_a_evap), size=14)
plt.show()

../_images/materials_241_heat_pump_system_28_0.png

COP of the heat pump system¶

\begin{align} COP = \frac{\dot{Q}_{cond}}{\dot{W}_{c} + \dot{W}_{cond,f} + \dot{W}_{evap,f}} \end{align}

In [16]:

COP = Q_dot_cond / (W_dot_c + params['W_dot_cond_f'] + params['W_dot_evap_f'])
display(COP)

2.895050928533937